Wat is Math Dungeon?
Een escape room voor twee spelers, voor 4 havo/vwo. Het spel heeft twee modussen, coöperatief (samenwerken om te ontsnappen) en competitief (wie ontsnapt het snelst). De spelers zitten in aparte kamers, waarin zij puzzels krijgen die opgelost moeten worden, om te kunnen ontsnappen uit de kamers.
De puzzels zijn op wiskunde gebaseerd, op zo’n manier dat de focus ligt op de fun tijdens het spelen en niet op het leren (maar dat gebeurt wel!).
De twee spelers komen in een dungeon terecht, ze kunnen elkaar niet zien, alleen horen, via hun ingebouwde communicatie systemen (de spelers zelf kunnen dus gewoon praten om te communiceren). Zij herkennen het als de catacombes van Parijs uit de boeken die ze hebben gelezen, echter herkennen ze deze specifieke catacombe niet. De spelers komen tijdens het spelen steeds meer te weten over het verhaal van deze speciale catacombe en ontmoeten uiteindelijk ook de necromancer die zich hier schuil houdt. Ze moeten onder andere door zijn laboratorium heen sluipen en komen erachter dat hij een horde ondoden los wil laten op de stad Parijs. Aan het einde moeten ze hem tegenhouden en de ondoden vernietigen. Doordat zij veel in de bibliotheek hebben gestudeerd, komen ze achter een ritueel waarmee ze hem en het ritueel waarmee hij de ondoden wilde oproepen kunnen stoppen en de ondoden weer naar het hiernamaals terug te sturen.
Het achtergrondverhaal
In het jaar 3204 leven robots onder de mensheid en werken ze voor de mensheid. De twee robots uit ons verhaal zijn aan het onderzoeken in een bibliotheek voor een onderzoeksproject waar zij aan meewerken. Plots vinden zij op een moeilijke plek (X), een boek dat er gloednieuw maar ook stoffig uitziet, alsof het geschreven is, maar daarna nooit meer is aangeraakt. Zij openen het boek uit nieuwsgierigheid en bladeren erdoorheen terwijl zij de oude tekeningen en teksten bewonderen. Al snel komen zij tot de conclusie dat het boek over de catacomben in Parijs gaat. De laatste paar pagina’s zijn, heel anders dan de rest van het boek, ruig en beschadigd, de meeste woorden zijn doorgekrast en zodra zij op de laatste pagina aankomen voelen zij opeens een kracht aan hen trekken. Zij zien nog snel een symbool in de tekening op deze pagina staan voordat zij in het boek gezogen worden. De speler ziet alleen nog het boek op de grond vallen, waarna er uitgezoomd wordt vanuit de bibliotheek. Het scherm wordt zwart en gaat over naar het spel.
Slideshow met screenshots van de game




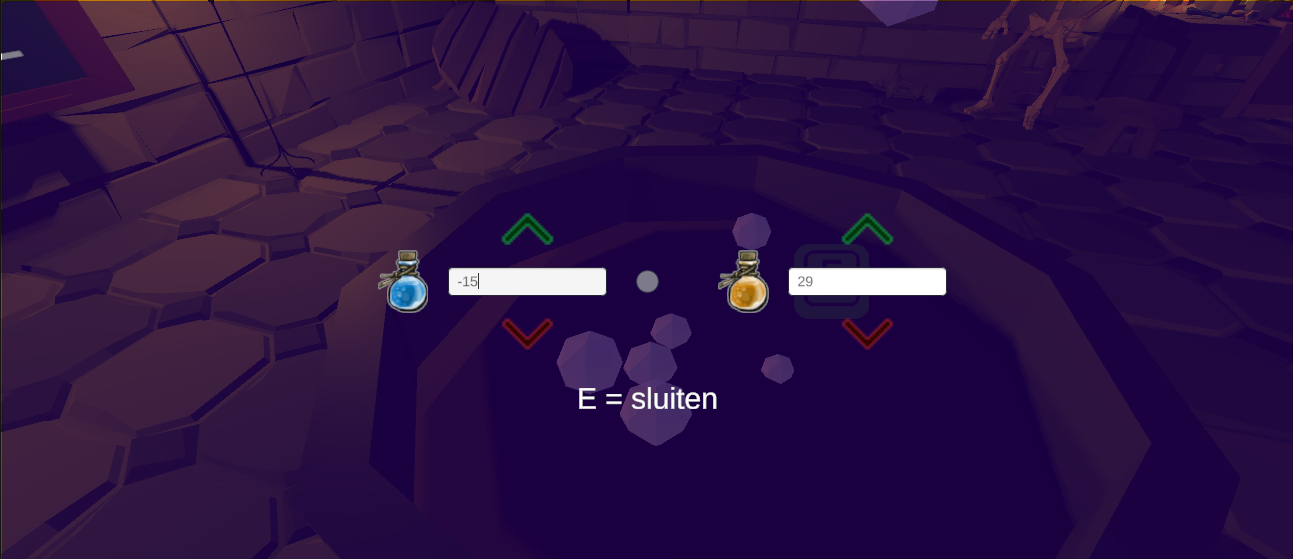



Video
Afstudeerrapport
Afstudeerpresentatie
Voorbeeld van één van de puzzels die ik heb ontworpen
Nadat de spelers elkaar weer hebben gevonden in de deurenpuzzel, raken zij elkaar toch weer kwijt. Uiteindelijk komt een van de spelers in een kamer terecht met een deur met tandwielen erop en de andere speler in een kamer met allemaal losse tandwielen.
Ook zien zij allebei een raam, met daarboven een getal. Zij kunnen elkaar ook zien door dit raam. Gelukkig zijn ze elkaar dus toch niet helemaal kwijt!
Tevens zien zij een deur, waardoor ze zeker weten dat er een uitweg mogelijk is en ze graag verder willen.
Het wiskundig doel van deze puzzel is:
- het oplossen van formules;
- het berekenen van snijpunten met de x-as;
- en vanuit snijpunten de formule berekenen.
Het speldoel van de puzzel is: tandwielen op de juiste plek zetten, waardoor er deuren openen en de spelers uit hun kamers kunnen ontsnappen.
In het linkerplaatje is een voorbeeld van de tandwielenpuzzel te zien, met de vergelijkingen op de grote tandwielen en de daarbij behorende snijpunten met de x-as op de kleine tandwielen.
Hoe werkt het:
Speler A vertelt speler B dat deze een muur ziet met daarop allemaal kleine tandwielen met getallen.
Speler B vertelt dan dat deze allemaal grote tandwielen met formules in de kamer ziet liggen.
Samen komen zij erachter dat de grote tandwielen tussen de kleine in gezet kunnen worden, met als link de vergelijkingen en hun snijpunten met de x-as.
Echter, zodra zij het eerste tandwiel doorgeven via het raam, zien zij het getal boven het raam verlagen.
- De reden hiervoor is dat er maar een maximaal aantal tandwielen mag worden doorgegeven door het raam, anders reset de kamer.
- Dit zorgt ervoor dat zij goed moeten nadenken welke tandwielen ze doorgeven en niet zomaar gaan brute-forcen.